Supercapacitors: The Key to Fast and Clean Energy Storage
We use molecular dynamics (MD) simulations to investigate the effects of the porosity of carbide-derived carbon-based electrodes and solvent concentration of a room-temperature ionic liquid (RTIL) electrolyte on electrochemical performance. At zero applied potential, the capacitance of the electric double-layer capacitor increased as the RTIL concentration increases for a porosity has a bigger diameter from the electrolyte molecules. For the lower porosities, it is observed that capacitance has the maximum value at the intermediate level of the RTIL concentration.
Introduction
An electric double-layer capacitor (EDLC), or a supercapacitor, is a high-power energy storage device, stores charge at the interface between carbon electrodes and an electrolyte solution.1 The charge storage is carried out by ion diffusion and adsorption at the electric surface or inside of the porous structure of the electrode. Since the energy in EDLCs is stored within their interfacial layers, the improvement of the energy density could be enabled by the increase of specific surface area (SSA) of the porous electrodes. 2 Based on this mechanism, the polarization of the electrode, and the choice of the electrolyte and electrode materials directly determine the electrical performances of EDLCs. They are highly promising for increment in power density with an advanced structure of electrode surface and electrolyte. Also, EDLCs have a higher cyclability and a faster charging rate than the batteries from the reason that the EDL structure is not accompanied by any chemical reaction.3
EDLCs using carbon nanomaterial as an electrode present excellent performance. Carbon nano-electrodes enlarge the electrode surface area in EDLCs to increase capacity and energy density.3 EDLC electrolytes are generally based on aqueous organic-based solvents. Room temperature ionic liquids (RTILs) are able to operate at extremely low temperatures and could conduct acceptable ionic conductivity, low vapor pressure, toxicity, and flammability, which makes them attractive candidates for EDLCs. When the addition of an aprotic solvent occurs, the solvent decreases the viscosity and increases the mobility of the electrolyte, which could lead to higher energy density for EDLCs.4
Models and Methods
The electrode material is chosen as carbon derived carbon. Carbide-derived carbons (CDCs), a family of nanoporous carbon, are usually produced by chlorination of metal or metalloid carbides at elevated temperatures. CDCs have gained special attention since they are adjustable for different porosity with high accuracy and narrow pore size distribution.5 The formation of micropores can be well controlled on an atomic level. The pore size of the CDCs is highly uniform due to the uniform distribution of carbon in the MC precursor.6
In the modeling of the electrode structure, Classic Molecular Dynamic (MD) simulations are used for microporous amorphous carbon. In the initial structure, the crystal structure of silicon carbide (SiC) was used, and it is followed by a pseudo-mimetic approach using quenched molecular dynamics (QMD).7 The SiC Tersoff potential is used in the simulations, which is available in the LAMMPS library. All our MD simulations were performed using LAMMPS program.8
Firstly, a 50 ps MD simulation was performed in the NVT ensemble at room temperature. It is continued by 200 ps NPT ensemble simulation at 2500 K. After that, the quenching is made from 2500 K to room temperature with a constant rate of 2.2 × 1012 K/s in the NPT ensemble. All Si atoms are removed from the systems for the simulation of chlorination. Finally, a 200 ps MD simulation in the NVT ensemble at room temperature was performed for stabilizing the remaining pure carbon structure.8 Then, for analyzing the pore size and pore distribution, Zeo++ is used in the determination of Specific Surface Area (SSA).9
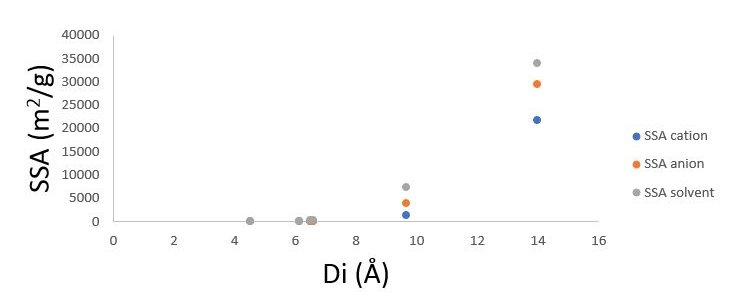
The porosity of the electrodes is determined as 4.5, 6.1, 6.5, 6.6, 9.6, and 13.9 angstrom. In the calculation of SSA, the radius of electrolyte molecules is taken as the base. As it is seen from Figure2.1, SSA has shown a tremendous increase with an increase in pore size. Electrodes with the porosity of 13.9 have shown extreme values for SSA measurements.
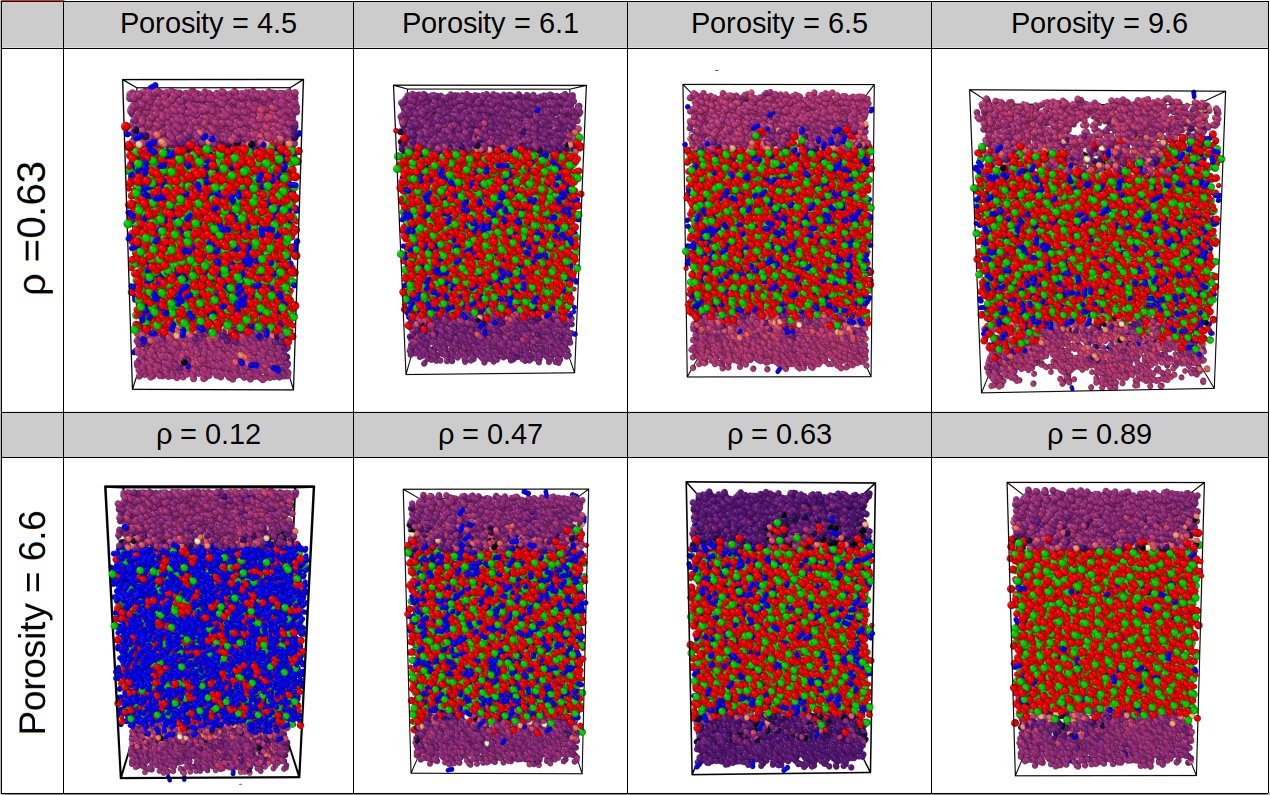
In our EDLC simulation systems, two parallel carbon derived carbon-based electrodes were used, and a mixture of 1-Butyl-3-methylimidazolium hexafluorophosphate [BMIM+] [PF6−] and acetonitrile (ACN) is used as an electrolyte. By using MD simulations in the constant potential ensemble, we investigate the effects of the porosity of carbide-derived carbon-based electrodes and the solvent concentration of a room temperature ionic liquid electrolyte on electrochemical performance. Different room temperature ionic liquid concentrations are chosen as 0.12, 0.47, 0.63, and 0.89 in terms of mole fractions. The system figures for the comparison has shown in Figure 2.2.
REFERENCES